Implicit integration methods
To obtain an implicit scheme, we introduce a little change in the 1st
order Taylor expansion used by Euler integration. In the equation below,
you can note that in the first line, forces are not expressed any more
at time t but at time t+1. This little change forces the
force field to be coherent at time t+1. We therefore assume that there will not be any unstability.
Theorically, this scheme is
stable whatever the time step and the spring constants are. The main drawback
is that we have to compute forces at time t+1, and cannot be computed directly.
To solve this problem, we use another first
order Taylor expansion to express forces at time t+1. Once done,
we reformulate the equation to obtain the final result specified in figure
below.
This is a linear equation system. We have to solve it in order
to find the velocity, and then the position of each node.
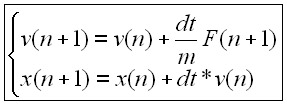


|














