Explicit integration methods
First of all, note that the fundamental dynamic equation is applicable
to each node. Each one has a position, a velocity and forces represented
by vectors. For this presentation, we use Euler explicit integration.
It consists in approximating the previous equation by a first
order Taylor expansion. Note that the dynamic fundamental equation,
which is a second order differential equation, was splitted into two first
order differential equations.
This method is very simple to implement but very instable. For a stable
system, we must choose a small time step
and small spring constants.
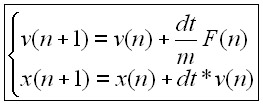
To resume,


|














